잔차연결(Residual Connection) 알아보기

잔차 연결(Residual Connection)은 깊은 신경망에서 발생하는 문제들을 해결하기 위해 도입된 기법입니다. 주요 특징과 장점은 다음과 같습니다:

개념

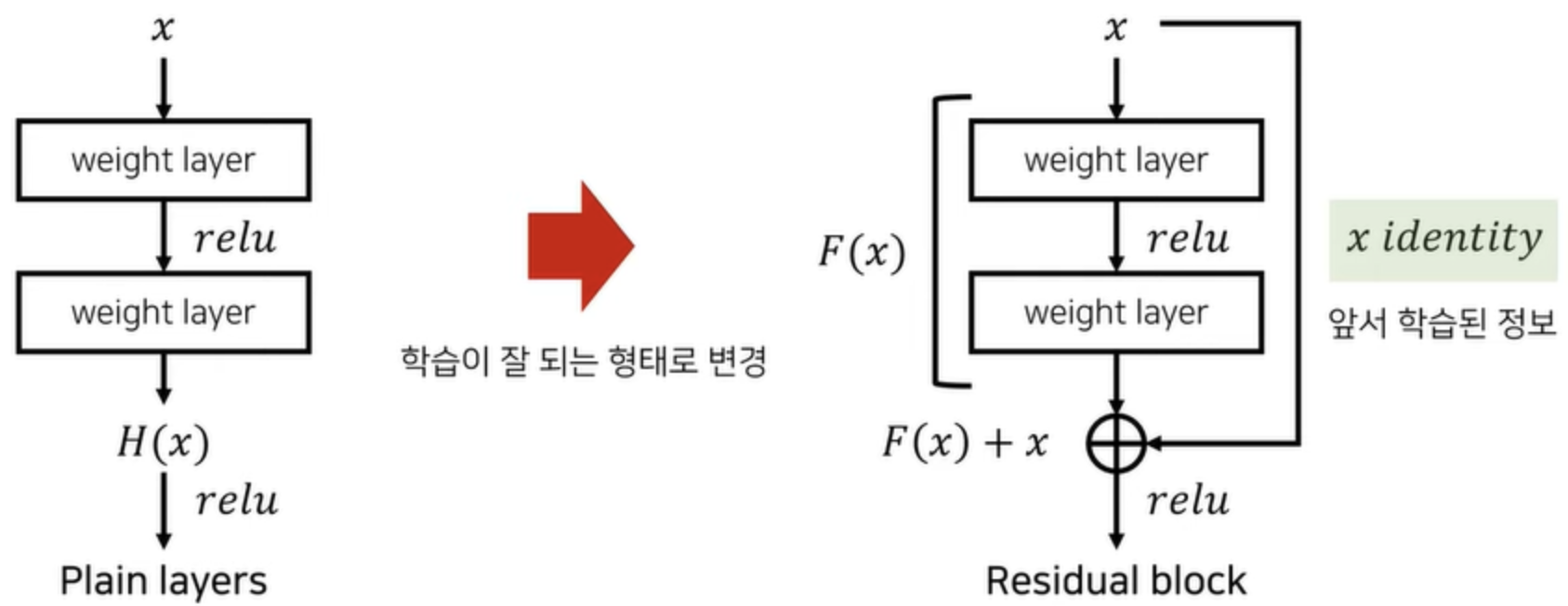
잔차 연결은 신경망의 특정 층의 입력을 그 층의 출력에 직접 더하는 방식으로 작동합니다. 수학적으로 표현하면 다음과 같습니다:

$$ H(x) = F(x) + x $$

여기서 x는 입력, F(x)는 해당 층에서 수행되는 변환, H(x)는 최종 출력입니다.

장점

1. 기울기 소실 문제 해결: 깊은 신경망에서 발생하는 기울기 소실 문제를 완화합니다[1][6].
2. 정보 보존: 이전 층의 정보를 직접적으로 다음 층으로 전달하여 중요한 특징들이 보존됩니다[2].
3. 학습 용이성: 네트워크가 잔차 함수 F(x)를 학습하게 되어, 최적화가 더 쉬워집니다[4].
4. 깊은 네트워크 구현: 수백 개의 층을 가진 매우 깊은 네트워크를 효과적으로 학습할 수 있게 합니다[5].

응용

• ResNet: 컴퓨터 비전 분야에서 널리 사용되는 ResNet 모델의 핵심 구성 요소입니다[7].
• Transformer: 자연어 처리 분야의 Transformer 모델에서도 잔차 연결이 중요한 역할을 합니다[11].

잔차 연결은 단순한 덧셈 연산만으로 구현되지만, 신경망의 성능을 크게 향상시키는 강력한 기법입니다. 이를 통해 더 깊고 복잡한 모델을 효과적으로 학습시킬 수 있게 되었습니다[10].

Citations:
[1] https://velog.io/@glad415/Transformer-7.-%EC%9E%94%EC%B0%A8%EC%97%B0%EA%B2%B0%EA%B3%BC-%EC%B8%B5-%EC%A0%95%EA%B7%9C%ED%99%94-by-WikiDocs
[2] https://brunch.co.kr/@26dbf56c3e594db/115
[3] https://sunway-light.tistory.com/8
[4] https://channelai.tistory.com/2
[5] https://daeun-computer-uneasy.tistory.com/28
[6] https://wikidocs.net/120073
[7] https://chickencat-jjanga.tistory.com/141
[8] https://blog.naver.com/chatghui/223624149237
[9] https://heeya-stupidbutstudying.tistory.com/entry/DL-Exploding-Vanishing-gradient-%EB%AC%B8%EC%A0%9C%EC%99%80-Residual-Connection%EC%9E%94%EC%B0%A8%EC%97%B0%EA%B2%B0
[10] https://lv99.tistory.com/25
[11] https://blog.naver.com/winddori2002/222008003445
[12] https://velog.io/@olxtar/Residual-BlockFunction-Connection
[13] https://meaningful96.github.io/deeplearning/skipconnection/